机器学习算法评估
由于 Ghost 博客对 LateX 的识别语法和标准的 LateX 语法有差异,为了更加通用性,所以以下文章中 LateX 公式可能出现乱码,如果出现乱码,不嫌弃的话可以在笔者的 Github 上看这篇无乱码的文章。笔者有空会修复这个乱码问题的。请见谅。
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub
Source: https://github.com/halfrost/Halfrost-Field/blob/master/contents/Machine_Learning/Advice_for_Applying_Machine_Learning.ipynb
一. Evaluating a Learning Algorithm
想要降低预测误差,即提高预测精度,我们往往会采用这些手段:
采集更多的样本
错误的认为样本越多越好,其实数据多并不是越好。降低特征维度
降维可能去掉了有用的特征。采集更多的特征
增加了计算负担,也可能导致过拟合。进行高次多项式回归
过高的多项式可能造成过拟合。调试正规化参数 $\lambda$,增大或者减少 $\lambda$
增大或者减少都是凭感觉。
有这么多种解决办法我们怎么知道是哪一种呢?很多人选择这些方法的标准就是凭感觉随便选择一种,然后花很长的时间最后发现是没用的,走上了不归路。所以下面我们介绍一我们需要一种简单有效的办法,我们将其称为机器学习算法诊断(Machine learning diagnostic)。
1. Evaluating a Hypothesis 评价假设函数
首先我们要评估的是我们的假设函数(Hypothesis)。当我们选择特征值或者参数来使训练集误差最小化,但是我们会遇到过拟合的问题,推广到新的训练集就不再使用了。而且当特征量很多的时候,我们就不能将 $J(\theta)$ 可视化看出其是否随着迭代次数而下降了。所以我们采用以下的方法来评估我们的假设函数:
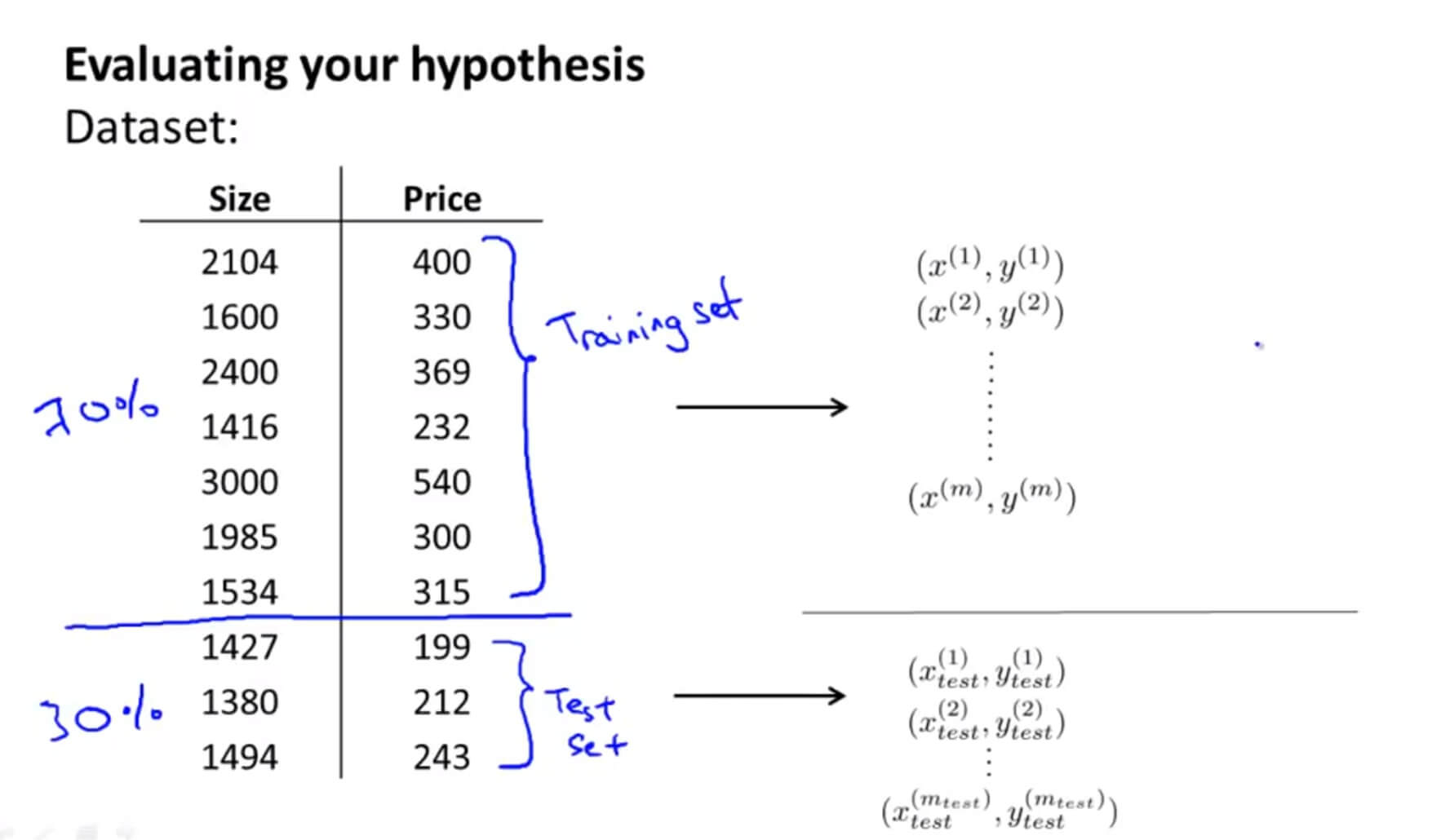
假设有 10 组数据,随机把 70% 做为训练集,剩下的 30% 做为测试集。训练集和测试集尽量保证是随机排列。
接下来:
- 对训练集进行学习得到参数 $\Theta$ ,也就是利用训练集最小化训练误差 $J_{train}(\Theta)$
- 计算出测试误差 $J_{test}(\Theta)$,取出之前从训练集中学习得到的参数 $\Theta$ 放在这里,来计算测试误差。
对于线性回归: $$J_{test}(\theta)=\frac{1}{2m_{test}}\sum_{i=1}^{m_{test}}{(h_\theta(x^{(i)}_{test})-y^{(i)}_{test})^2}$$
对于逻辑回归: $$J_{test}(\theta)=-\frac{1}{m_{test}}\sum_{i=1}^{m_{test}}{y^{(i)}_{test}logh_\theta(x^{(i)}_{test})+(1-y^{(i)}_{test})logh_\theta(x^{(i)}_{test})}$$
逻辑回归不同于线性回归,因为它只有0和1两个值, 所以怎么判断误差如下:
$$ err(h_\theta(x),y)=\left{\begin{matrix} 1 ;;;( if ;;; h_\theta(x) \geqslant 0.5 , y=0 ;;;or;;; if;;; h_\theta(x) < 0.5 , y=1 )\ 0 ;;;( otherwise ) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; \end{matrix}\right. $$
这里的误差也叫误分类率,也叫 $0/1$ 错分率。
$( if ;;; h_\theta(x) \geqslant 0.5 , y=0 ;;;or;;; if;;; h_\theta(x) < 0.5 , y=1 )$
这种情况下,假设结果更趋向于1,但是实际给出的判断却是0,或者假设结果更趋向于0,实际给出的判断却是1 。
如果以上情况都没有,那么就没有误差,即为0 ,也代表了假设值能够正确的对样本进行分类。
测试集的平均测试误差为:
$$Test;Error=\frac{1}{m_{test}}\sum_{i=1}^{m_{test}}err(h_{\theta}(x^{(i)}_{test}),y^{(i)}_{test})$$
2. Model Selection and Train/Validation/Test Sets 模型选择和训练集/验证集/测试集

我们这里用 d 表示多项式的个数。我们可以改变多项式次数的多少来选择合适我们的模型。例如上面的 $h_\theta(x)=\theta_0+\theta_1x$ ,这个多项式 $d=1$ 。
我们可以测试每一个模型得到他们的 $J_{test}(\theta)$ ,判断哪一个模型比较好。
当选择出了一个多项式 d 能很完美的拟合测试集,接下来就不能再用测试集了,因为 d 本来就已经完美拟合测试集了,再测试就没有意义了,需要换一个测试集。所以更需要关心的对新样本的拟合效果。
为了解决上述问题,我们把数据分为 3 类,训练集 60% /交叉验证集 20% /测试集 20%。
通过三个集合,可以算出训练误差:
$$J_{train}(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^{2}$$
交叉验证误差:
$$J_{cv}(\theta) = \frac{1}{2m_{cv}}\sum_{i=1}^{m_{cv}}(h_\theta(x^{(i)}_{cv})-y^{(i)}_{cv})^{2}$$
测试误差:
$$J_{test}(\theta) = \frac{1}{2m_{test}}\sum_{i=1}^{m}(h_\theta(x^{(i)}_{test})-y^{(i)}_{test})^{2}$$
于是我们选择模型不在仅仅通过测试集来选择了,而是:
- 利用训练集的数据代入每一个多项式模型。
- 用交叉验证集的数据找出最小误差的多项式模型。
- 最后在测试集再找出相对较少误差的那个模型。
二. Bias vs. Variance
1. Diagnosing Bias vs. Variance 诊断偏差和方差
在机器学习中,偏差(bias)反映了模型无法描述数据规律,而方差(variance)反映了模型对训练集过度敏感,而丢失了数据规律,高偏差和高方差都会造成新数据到来时,模型给出错误的预测。
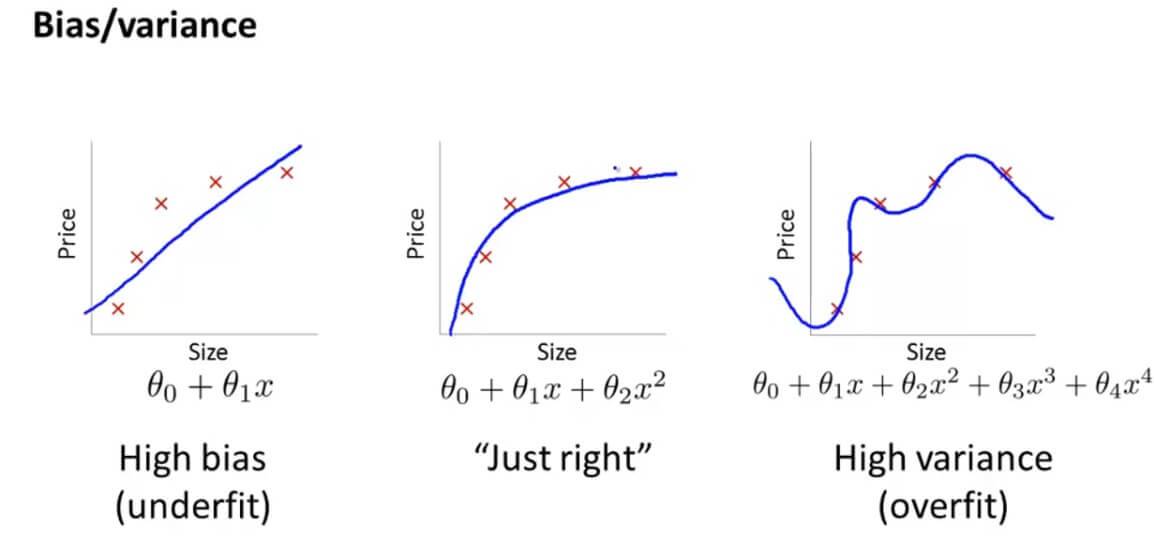
还是以这个图为例,最左边的图是欠拟合,最右边的图是过拟合。
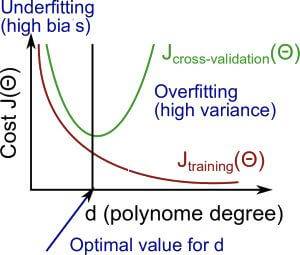
上图是 训练集、交叉验证集误差随多项式次数 d 的变化规律。横坐标是我们的d,也就是多项式的个数,纵坐标就是我们的代价函数。
我们先来看一下红色曲线 $J_{training}(\theta)$ ,随着多项式个数的增加,其假设函数是越来越接近要拟合的数据,所以其代价函数会随着多项式个数的增加下降。
然后绿色的曲线是 $J_{cross-validation}(\theta)$ ,当多项式个数比较少的时候,那当然会出现欠拟合的现象,所以一开始其代价函数 $J_{cross-validation}(\theta)$ 是很大的,随着多项式个数的增加而下降,但是当其多项式个数再继续增加的话,就会出现过拟合的现象, $J_{cross-validation}(\theta)$ 就又会增加。所以 $J_{cross-validation}(\theta)$ 函数是先递减再递增的,在其最低点就是最合适的多项式次数。
多项式回归中,如果多项式次数较高,则容易造成过拟合,此时训练误差很低,但是对于新数据的泛化能力较差,导致交叉验证集和测试集的误差都很高,此时模型出现了高方差(过拟合):
$$ \left{\begin{matrix} J_{train}(\theta) ;;;is;; low\ J_{cv}(\theta)»J_{test}(\theta) \end{matrix}\right. $$
过拟合的情况下,训练集误差通常比较小,并且远小于交叉验证误差。
而当次数较低时,又易出现欠拟合的状况,此时无论是训练集,交叉验证集,还是测试集,都会有很高的误差,此时模型出现了高偏差(欠拟合):
$$ \left{\begin{matrix} J_{train}(\theta),J_{cv}(\theta);;; is ;; high\ J_{cv}(\theta) \approx J_{test}(\theta) \end{matrix}\right. $$
欠拟合的情况下,训练集误差会很大。
为什么 $J_{cross-validation}(\theta)$ 会先降后升,而 $J_{training}(\theta)$ 一直下降?
原因是 $\theta$ 是只针对训练集所训练出来的,当其代入到 $J_{cross-validation}(\theta)$ 后,就会随着多项式的增加数据偏差就会越来越大。
2. Regularization and Bias/Variance 正则化的偏差和方差
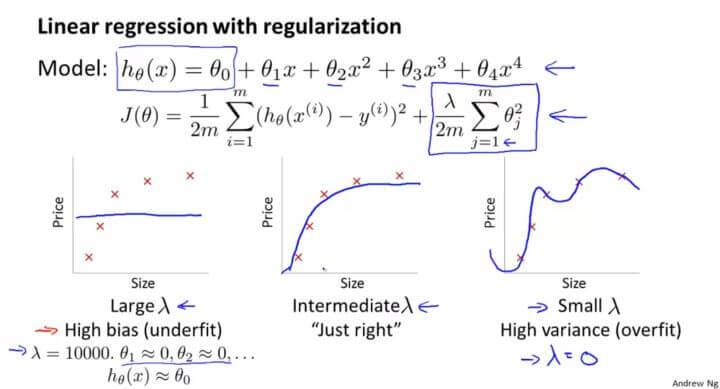
为了防止过拟合的现象,我们加上一个正则化项,但是正则化参数 $\lambda$ 与过拟合又有什么关系呢?
当 $\lambda$ 很大的时候,就会使得后面的每一个 $\theta_i$ 都被惩罚了,所以只剩下 $\theta_0$ ,那么其假设函数就会变成一条直线,出现欠拟合的现象。
当 $\lambda$ 很小的话,一个极端例子就是 $\lambda=0$ ,也就是相当于没有加正则化那项,这就会导致过拟合的现象。
$\lambda$的取值不能过大也不能过小。
$\lambda$的取值可以在 $\left[0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24\right]$,在这12个不同的模型中针对每一个 $\lambda$ 的值,都去计算出一个最小代价函数,从而得到 $\Theta^{(i)}$
得到了12个 $\Theta^{(i)}$ 以后,就再用交叉验证集去评价它们。即计算每个 $\Theta$ 在交叉验证集上的平均误差平方和 $J_{cv}(\Theta^{(i)})$
选择一个交叉验证集误差最小的 $\lambda$ 最能拟合数据的作为正则化参数。
最后拿这个正则化参数去测试集里面验证 $J_{test}(\Theta^{(i)})$ 预测效果如何。
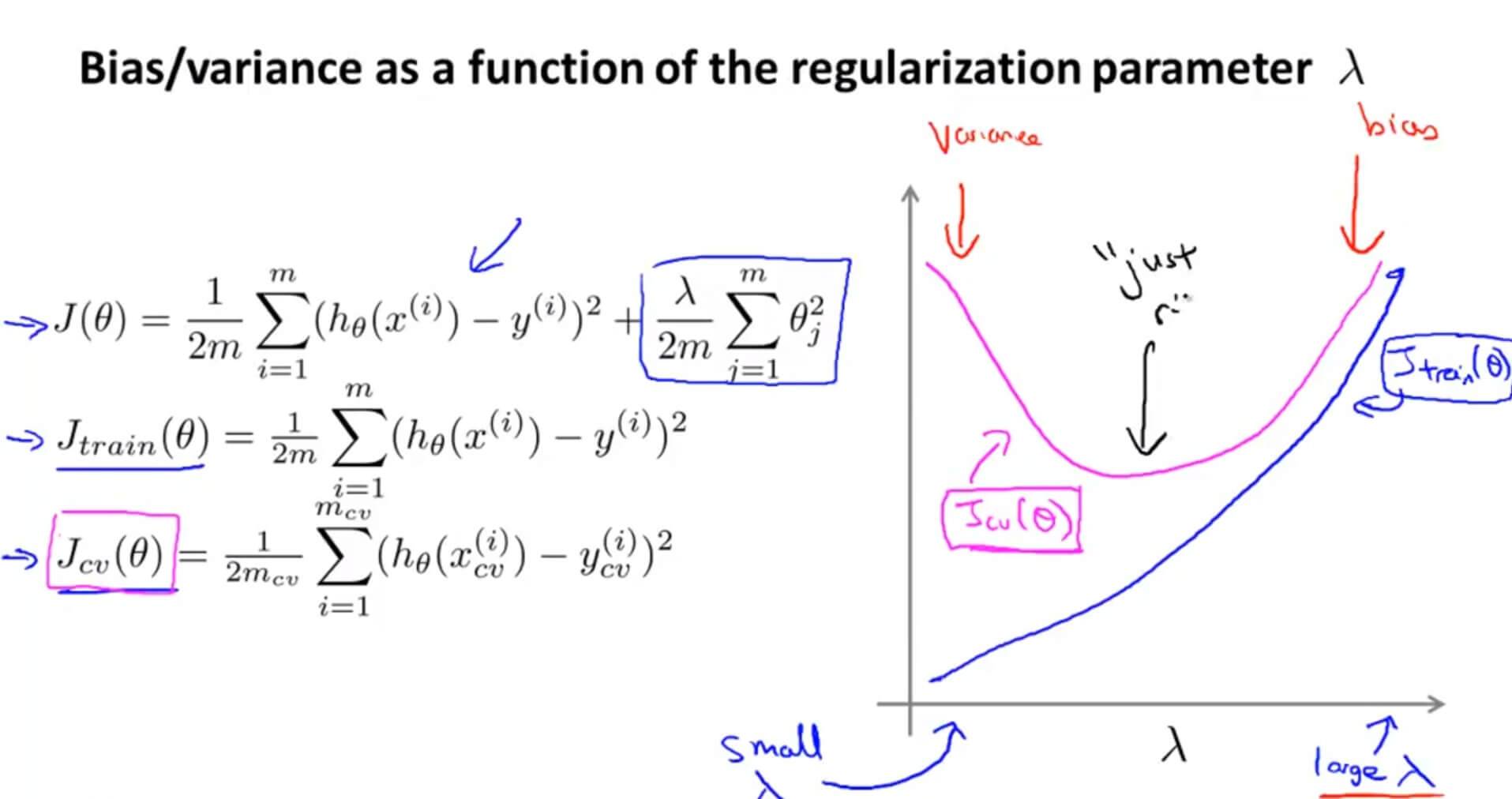
随着 $\lambda$ 参数的增大, $J_{train}(\theta)$ 自然也会随之增大,这是因为当 $\lambda=0$ 的时候, $J_{train}(\theta)$ 是没有正则化项的。
但是对于 $J_{cv}(\theta)$ 来说,它假设函数里面的 $\theta$ 是根据训练集里面拟合出来的,所以在没有加入正则化前, $J_{cv}(\theta)$ 是很大的。但是随着 $\lambda$ 的逐渐增大,也就是随着正则化的效果逐渐体现出来,在交叉验证集里面与测试数据就会越来越拟合,这时候的 $J_{cv}(\theta)$ 自然会慢慢下降。但是当 $\lambda$ 变得足够大的时候,交叉训练集的 $h_\theta(x)$ 就会趋近一条直线,$J_{cv}(\theta)$ 自然会随之上升。
3. Learning Curves 学习曲线
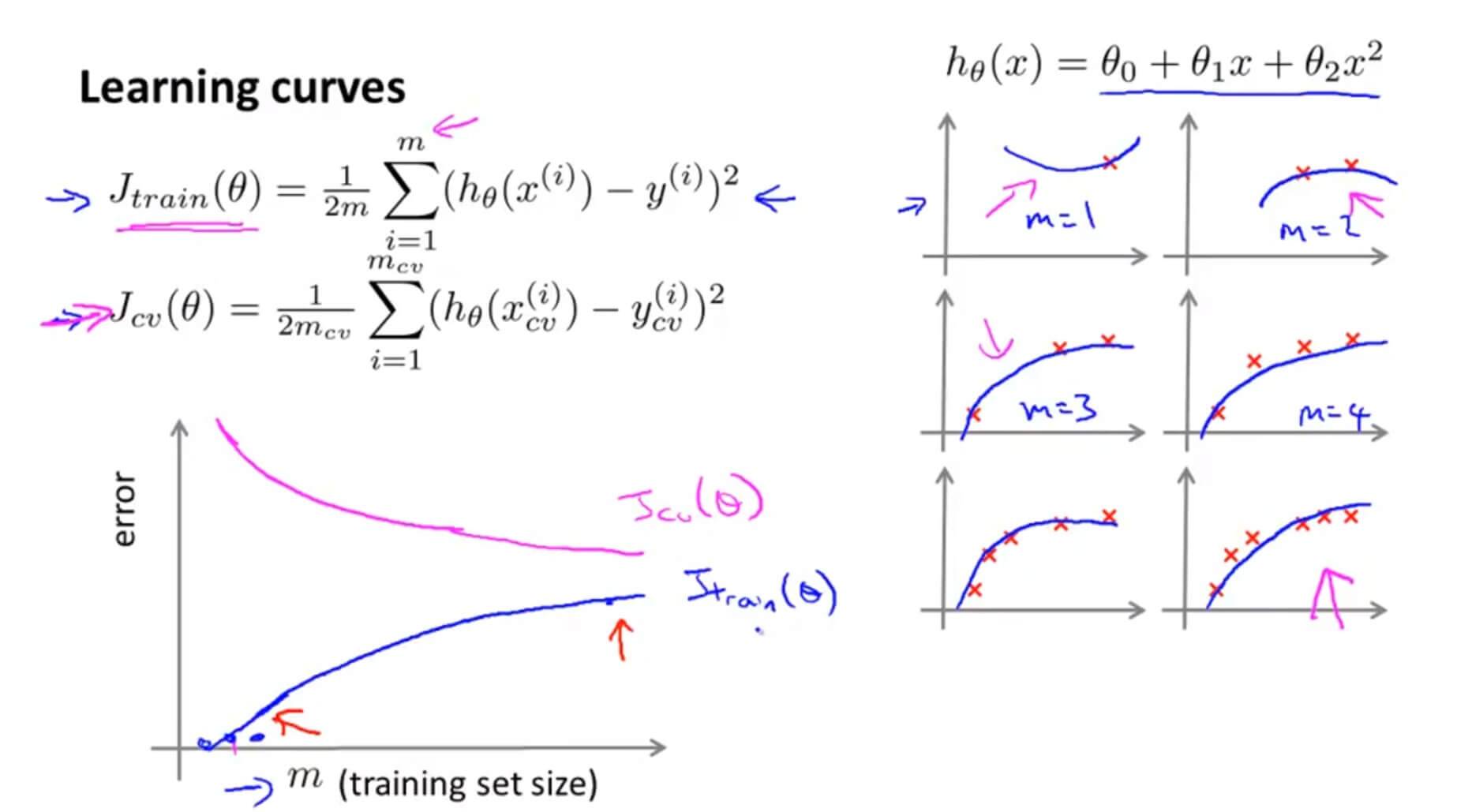
假设我们用 $h_\theta(x)=\theta_0+\theta_1x+\theta_2x^2$ 去拟合数据,当数据只有几个的时候,拟合效果那肯定的非常好的,但是,当数据越来越多,我们的假设函数因为多项式太少就不能很好地拟合数据了。所以训练集的误差 $J_{train}(\theta)$ 会随着数据的增多而增大。如上图蓝色的曲线。
但是对于交叉验证集呢?因为一开始只有几个数据,那么在训练集拟合出来的参数就有很大的可能不适合交叉验证集,所以在数据很小的情况下其误差是很大的,但是随着数据的慢慢增多,虽然个别的数据拟合不上,但是整体的拟合效果那肯定比只有几个数据的时候好了,所以其整体误差是逐步下降的。如上图粉色的曲线。
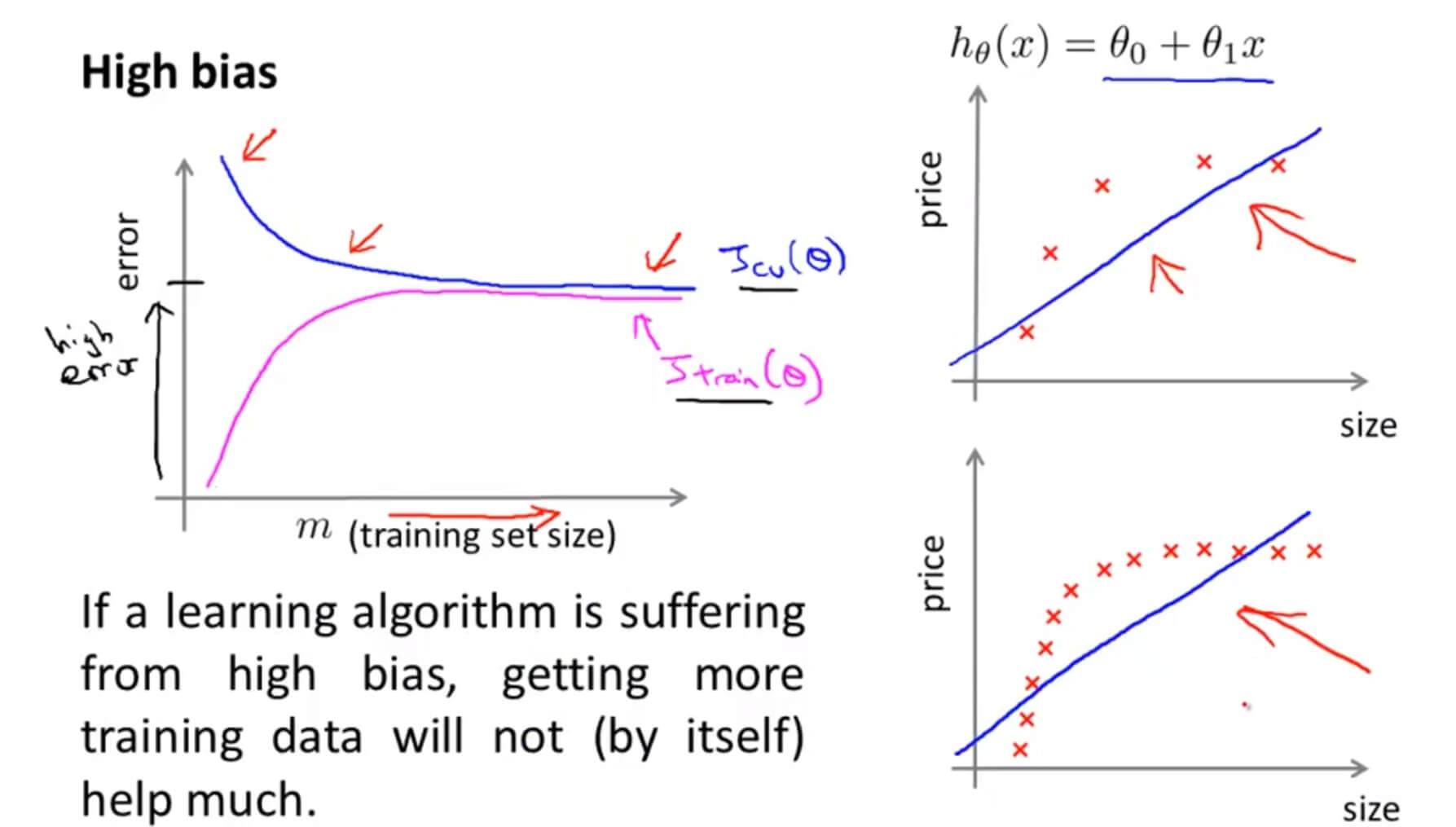
当数据存在高偏差也就是欠拟合的时候,即使数据再继续增多也无补于事,所以其误差会趋于一个平衡的位置,而且 $J_{train}(\theta)$ 和 $J_{cv}(\theta)$ 的误差都会很大。
所以,当数据存在欠拟合的问题,我们选用更多的训练样本是没有办法解决问题的。
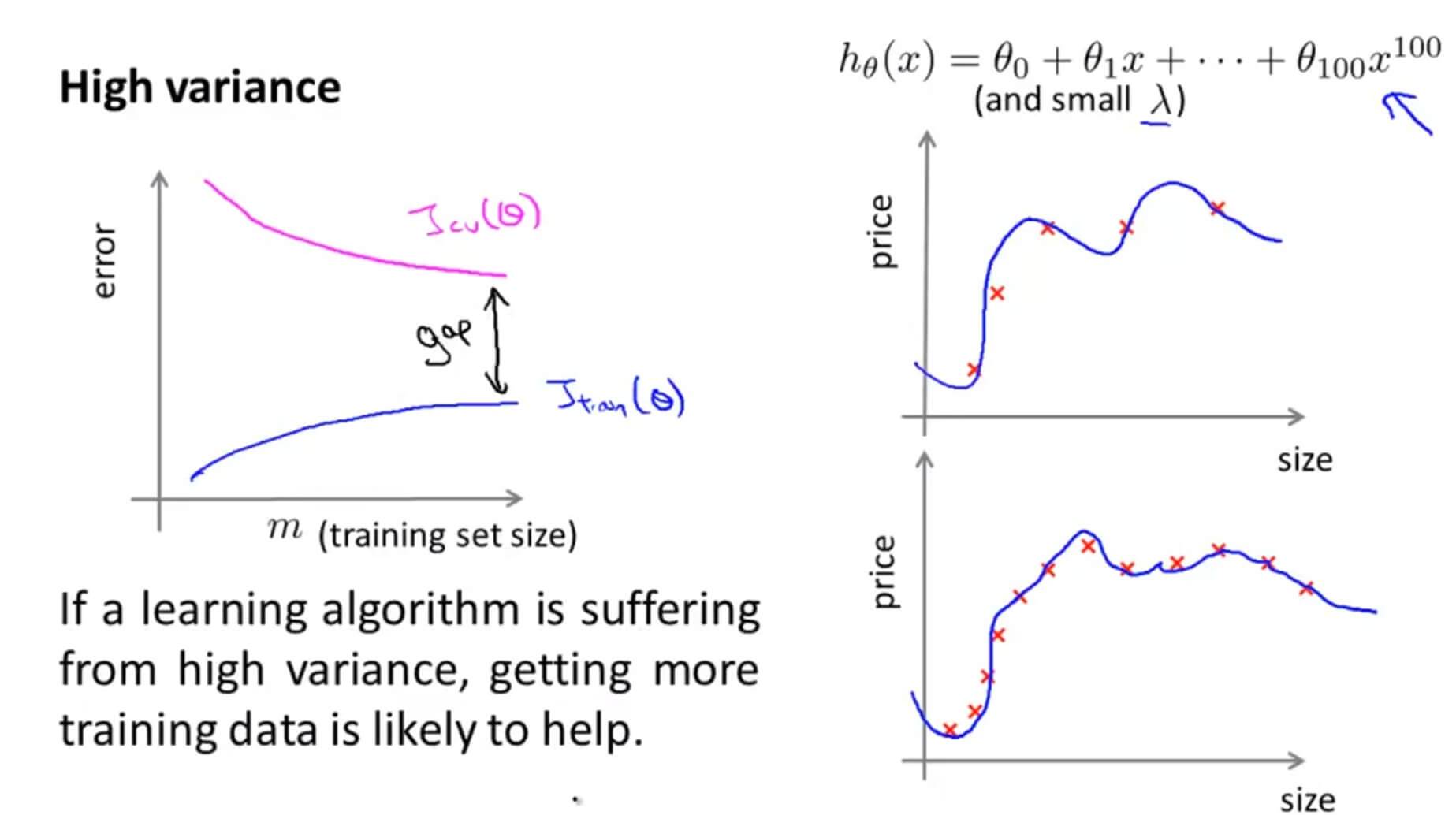
当数据存在高方差也就是过拟合的时候,随着数据的增多,因为过拟合所以在训练集基本能完美拟合其数据,所以训练集的误差虽然会上升,但是其幅度是非常缓慢的,在交叉验证集也一样,所以过拟合的时候其图像如上,在 $J_{train}(\theta)$ 和 $J_{cv}(\theta)$ 之间有一大段空隙。
所以,当数据存在过拟合的现象,选用更多的样本有利于我们解决这个问题。
4. Deciding What to Do Next Revisited 决定下一步该做什么
总结 :
| 手段 | 使用场景 |
|---|---|
| 采集更多的样本 | 高方差(过拟合) |
| 降低特征维度 | 高方差(过拟合) |
| 采集更多的特征 | 高偏差(欠拟合) |
| 进行高次多项式回归 | 高偏差(欠拟合) |
| 降低参数 λ | 高偏差(欠拟合) |
| 增大参数 λ | 高方差(过拟合) |
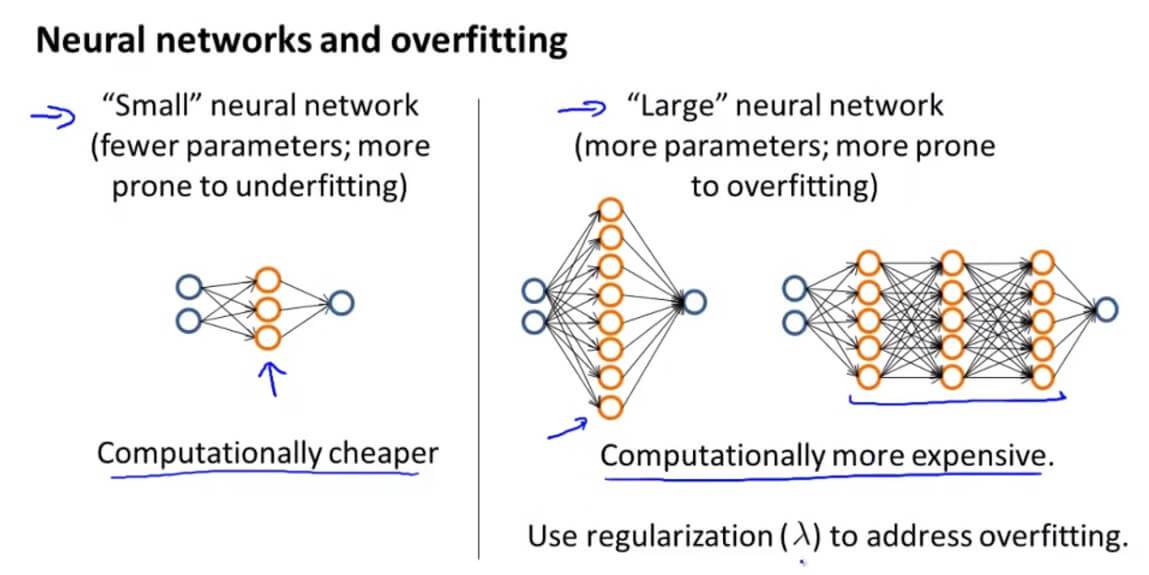
当我们选用一些较小的神经网络,虽然其计算量较少,但是容易出现欠拟合的现象。相反,我们选用一些层数比较多,层的单元比较多的神经网络,容易出现过拟合的现象。我们之前提到越大型的神经网络效果越好,为了防止出现过拟合的现象,我们可以使用正则化的方法来修正。
使用单个隐藏层是一个很好的默认开始。您可以使用交叉验证集在许多隐藏层上训练您的神经网络。然后您可以选择性能最好的一个。
模型复杂性影响:
- 低阶多项式(低模型复杂度)具有高偏差和低方差。在这种情况下,该模型很难一致
- 高阶多项式(高模型复杂度)非常适合训练数据,测试数据极其糟糕。这些对训练数据的偏倚低,但差异很大
- 实际上,我们希望选择一个介于两者之间的模型,它可以很好地推广,但也可以很好地适合数据。
三. Advice for Applying Machine Learning 测试
1. Question 1
You train a learning algorithm, and find that it has unacceptably high error on the test set. You plot the learning curve, and obtain the figure below. Is the algorithm suffering from high bias, high variance, or neither?

A. High variance
B. Neither
C. High bias
解答:A
高方差的图像
2. Question 2
Suppose you have implemented regularized logistic regression to classify what object is in an image (i.e., to do object recognition). However, when you test your hypothesis on a new set of images, you find that it makes unacceptably large errors with its predictions on the new images. However, your hypothesis performs well (has low error) on the training set. Which of the following are promising steps to take? Check all that apply.
A. Try adding polynomial features.
B. Get more training examples.
C. Try using a smaller set of features.
D. Use fewer training examples.
解答:B、C
过拟合可以减少特征量和增加训练样本数量,或者增大正则化参数 $\lambda$ 。
3. Question 3
Suppose you have implemented regularized logistic regression to predict what items customers will purchase on a web shopping site. However, when you test your hypothesis on a new set of customers, you find that it makes unacceptably large errors in its predictions. Furthermore, the hypothesis performs poorly on the training set. Which of the following might be promising steps to take? Check all that apply.
A. Try using a smaller set of features.
B. Try adding polynomial features.
C. Try to obtain and use additional features.
D. Try increasing the regularization parameter $\lambda$.
解答:B、C
欠拟合可以增加特征量和假设函数的多项式。
4. Question 4
Which of the following statements are true? Check all that apply.
A. Suppose you are training a regularized linear regression model. The recommended way to choose what value of regularization parameter $\lambda$ to use is to choose the value of $\lambda$ which gives the lowest test set error.
B. The performance of a learning algorithm on the training set will typically be better than its performance on the test set.
C. Suppose you are training a regularized linear regression model.The recommended way to choose what value of regularization parameter $\lambda$ to use is to choose the value of $\lambda$ which gives the lowest training set error.
D. Suppose you are training a regularized linear regression model. The recommended way to choose what value of regularization parameter $\lambda$ to use is to choose the value of $\lambda$ which gives the lowest cross validation error.
解答:B、D
在正则化线性回归中,$\lambda$ 选择一个交叉验证集误差最小的 λλ 最能拟合数据的作为正则化参数。
5. Question 5
Which of the following statements are true? Check all that apply.
A. If a learning algorithm is suffering from high variance, adding more training examples is likely to improve the test error.
B. We always prefer models with high variance (over those with high bias) as they will able to better fit the training set.
C. If a learning algorithm is suffering from high bias, only adding more training examples may not improve the test error significantly.
D. When debugging learning algorithms, it is useful to plot a learning curve to understand if there is a high bias or high variance problem.
解答:A、C、D
A 过拟合高方差,增加样本数量有用。
B 高偏差和高方差的模型都不好。
C 增加训练样本对于欠拟合是没用的正确。
D 绘制学习曲线有利于帮助我们分析问题正确。
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub
