无监督学习
由于 Ghost 博客对 LateX 的识别语法和标准的 LateX 语法有差异,为了更加通用性,所以以下文章中 LateX 公式可能出现乱码,如果出现乱码,不嫌弃的话可以在笔者的 Github 上看这篇无乱码的文章。笔者有空会修复这个乱码问题的。请见谅。
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub
Source: https://github.com/halfrost/Halfrost-Field/blob/master/contents/Machine_Learning/Unsupervised_Learning.ipynb
一. Clustering
1. 定义
从本节开始,将正式进入到无监督学习(Unsupervised Learning)部分。无监督学习,顾名思义,就是不受监督的学习,一种自由的学习方式。该学习方式不需要先验知识进行指导,而是不断地自我认知,自我巩固,最后进行自我归纳,在机器学习中,无监督学习可以被简单理解为不为训练集提供对应的类别标识(label),其与有监督学习的对比如下:
有监督学习(Supervised Learning)下的训练集:
$$\left{ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(m)},y^{(m)}) \right}$$
无监督学习(Unsupervised Learning)下的训练集:
$$\left{ (x^{(1)}),(x^{(2)}),(x^{(3)}),\cdots,(x^{(m)}) \right}$$

在有监督学习中,我们把对样本进行分类的过程称之为分类(Classification),而在无监督学习中,我们将物体被划分到不同集合的过程称之为聚类(Clustering)。聚这个动词十分精确,他传神地描绘了各个物体自主地想属于自己的集合靠拢的过程。
在聚类中,我们把物体所在的集合称之为簇(cluster)。
2. K-Means
在聚类问题中,我们需要将未加标签的数据通过算法自动分成有紧密关系的子集。那么K均值聚类算法(K-mean)是现在最为广泛使用的聚类方法。
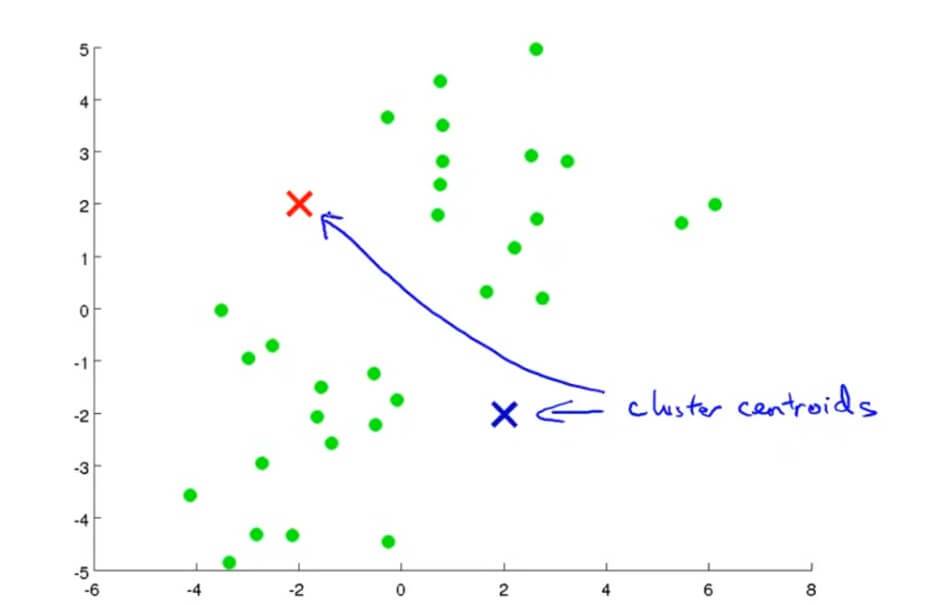
我们执行K均值聚类算法是这样的。首先随机选择两个点,这两个点叫做聚类中心(cluster centroids),也就是图中红色和蓝色的交叉。K均值聚类 一个迭代的方法,它要做两件事,一件是簇分配,另一件是移动聚类中心。
在K均值聚类算法的每次循环里面,第一步要进行的是簇分配。首先要历遍所有的样本,也就是上图中每一个绿色的点,然后根据每一个点是更接近红色的这个中心还是蓝色的这个中心,将每一个数据点分配到两个不同的聚类中心。
例如第一次我们随机定的两个中心点和其簇分配如下图所示:
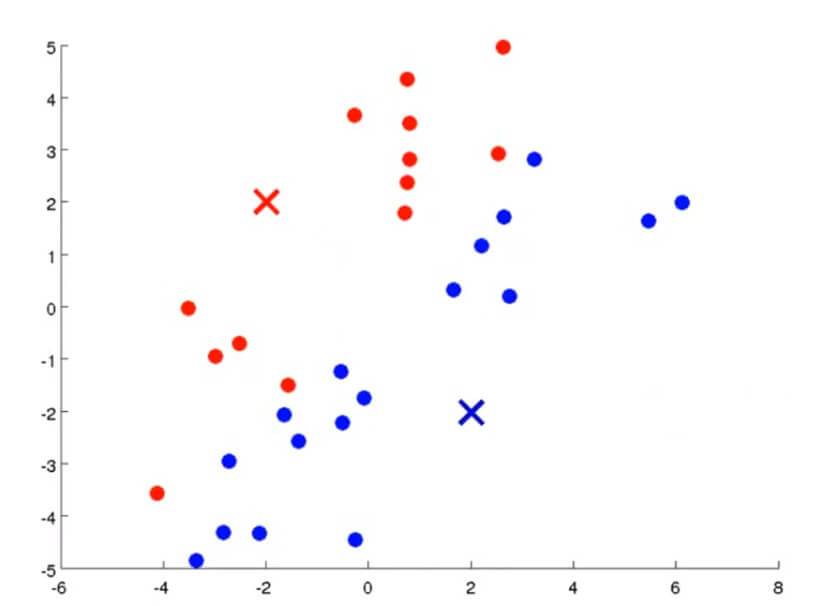
第二步要做的自然是要移动聚类中心。我们需要将两个中心点移动到刚才我们分成两类的数据各自的均值处。那么所要做的就是找出所有红色的点计算出他们的均值,然后把红色叉叉移动到该均值处,蓝色叉叉亦然。
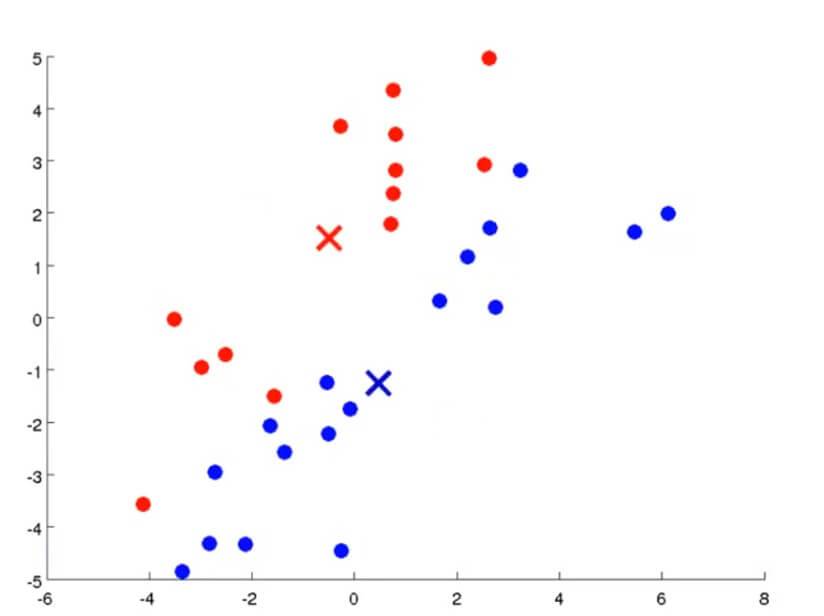
然后通过不断重复上述两个步骤,通过不断迭代直到其聚类中心不变,那么也就是说K均值聚类已经收敛了,我们就可以从该数据中找到两个最有关联的簇了。其过程大概如下图所示:
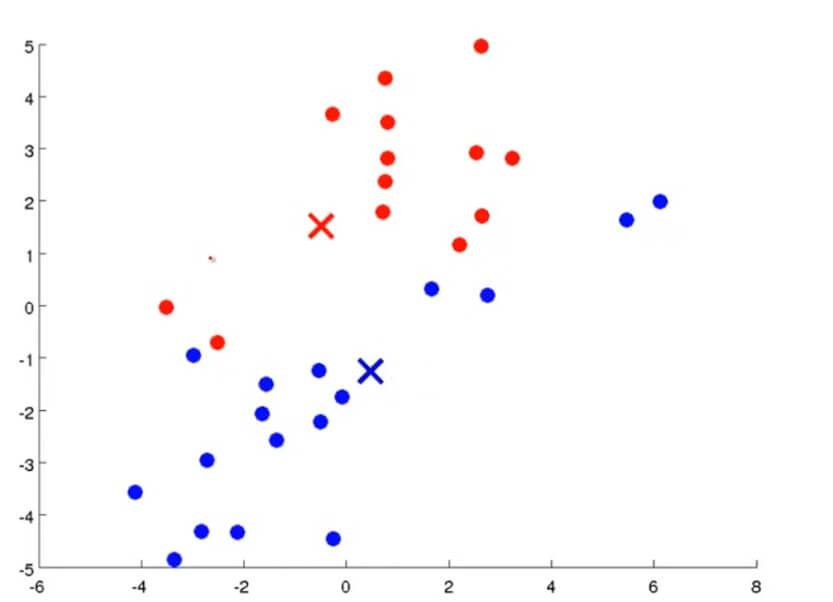

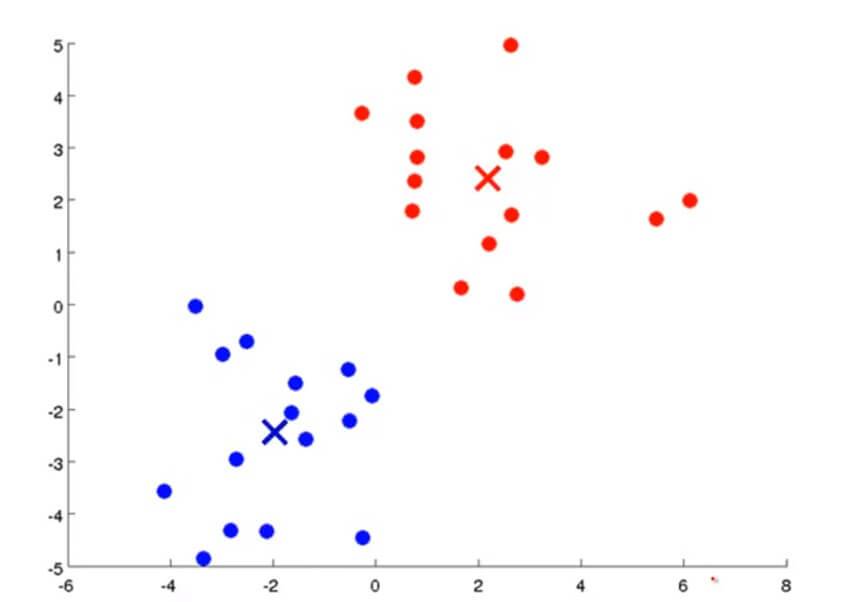
K均值聚类算法有两个输入:一个是参数K,也就是你想从数据中聚类出簇的个数。另一个就是只有x没有y的训练集。
以下是 K 均值聚类算法的过程。
第一步是随机初始化K个聚类中心,记做: $\mu_1, \mu_2,\cdots,\mu_k$ 。
第二个大部分就是进行迭代。其中第一个循环是:对于每个训练样本 ,我们用变量 $c^{(i)}$ 表示在 K 个聚类中心里面最接近 $x^{(i)}$ 那个中心的下标。我们可以通过 $min_k||x^{(i)}-\mu_k||$ 进行计算。第二个循环是:移动聚类中心。将 $\mu_k$ 也就是中心点的值 = 刚才我们分好的簇的均值。
例如: $\mu_2$ 被分配到一些样本值: $x^{(1)},x^{(5)},x^{(6)},x^{(10)}$ 。这也就意味着: $c^{(1)}=2,c^{(5)}=2,c^{(6)}=2,c^{(10)}=2$ 。那么 $\mu_2$ 的新值应该为: $\frac{1}{4}[ x^{(1)}+x^{(5)}+x^{(6)}+x^{(10)}]$ 。
3. 优化
和其他机器学习算法一样,K-Means 也要评估并且最小化聚类代价,在引入 K-Means 的代价函数之前,先引入如下定义:
$\mu^{(i)}_c$=样本 $x^{(i)}$ 被分配到的聚类中心
引入代价函数:
$$J(c^{(1)},c^{(2)},\cdots,c^{(m)};\mu_1,\mu_2,\cdots,\mu_k)=\frac{1}{m}\sum_{i=1}^m\left | x^{(i)}-\mu_c(i) \right |^2$$
J 也被称为失真代价函数(Distortion Cost Function),可以在调试K均值聚类计算的时候可以看其是否收敛来判断算法是否正常工作。
实际上,K-Means 的两步已经完成了最小化代价函数的过程:
- 样本分配时:
我们固定住了 $(\mu_1,\mu_2,\cdots,\mu_k)$ ,而关于 $(c^{(1)},c^{(2)},\cdots,c^{(m)})$ 最小化了 J 。
- 中心移动时:
我们再关于 $(\mu_1,\mu_2,\cdots,\mu_k)$ 最小化了 J 。
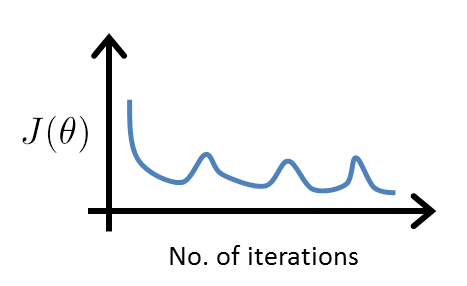
由于 K-Means 每次迭代过程都在最小化 J ,所以下面的代价函数变化曲线不会出现:
4. 如何初始化聚类中心
当我们运行K均值算法的时候,其聚类中心K的值要少于样本总数m。
然后我们随便选K个训练样本作为聚类中心。例如K=2的时候,如右图,随便选取那两个训练样本作为两个不同的聚类中心。
但是这样随便选的话,会造成K均值落在局部最优不好的结果。
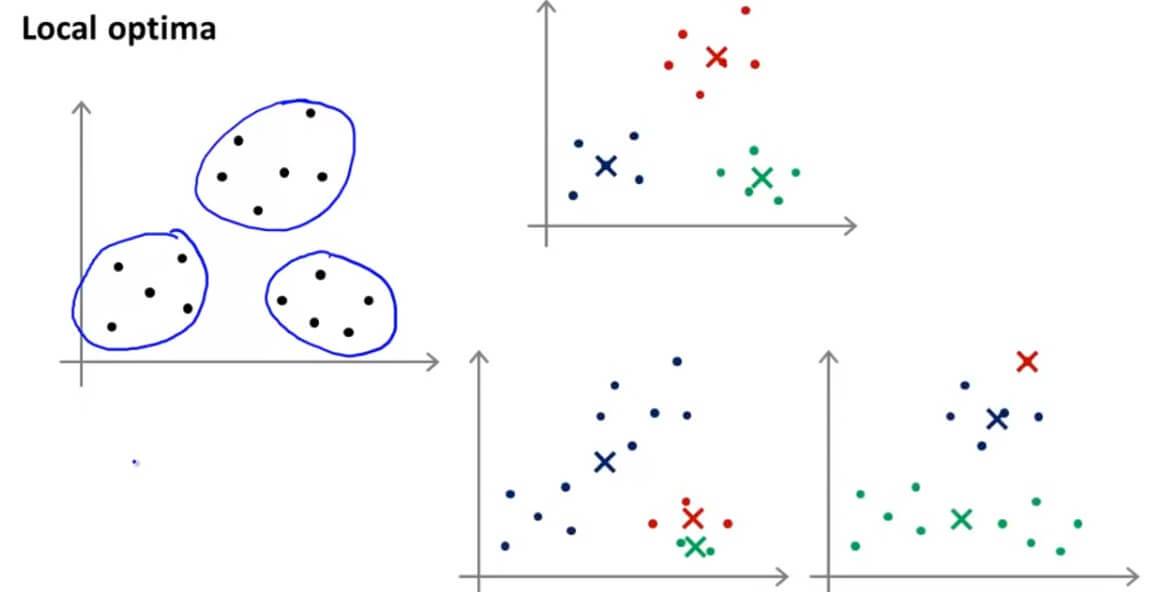
例如,我们给出左图的数据,很容易看出可以分成3个聚类,但是因为随机初始化不好的时候,会落入到局部最优而不是全局最优。也就是右下图的两种情况。
所以我们随机初始化的操作如下:

通常,我们会随机选 K 个样本作为 K 个聚类中心 ( K<m )。但是,如下图所示,不同的初始化有可能引起不同的聚类结果,能达到全局最优(global optimal)固然是好的,但是,往往得到的是局部最优(local optimal)。
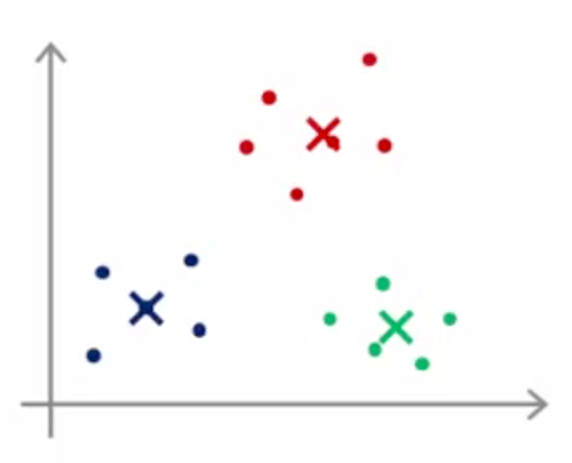
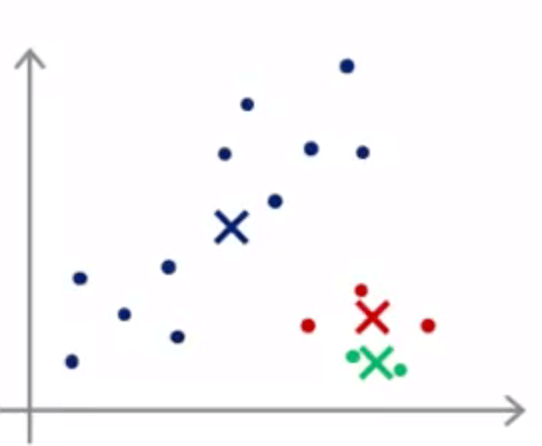
现在,想要提前避免不好的聚类结果仍是困难的,我们只能尝试不同的初始化:
for i=1 to 100 :
- 随机初始化,执行 K-Means,得到每个所属的簇 $c^{(i)}$ ,以及各聚类的中心位置 $\mu$ : $$c^{(1)},c^{(2)},\cdots,c^{(m)};\mu_1,\mu_2,\cdots,\mu_k$$
- 计算失真函数 J
选择这 100 次中, J 最小的作为最终的聚类结果。
随机选取K值,但是要循环不重复取100次,取其 $J(c^{(1)},c^{(2)},\cdots,c^{(m)};\mu_1,\mu_2,\cdots,\mu_k)$ 最低的那个结果。
5. 如何确定聚类数
肘部法则(Elbow Method):
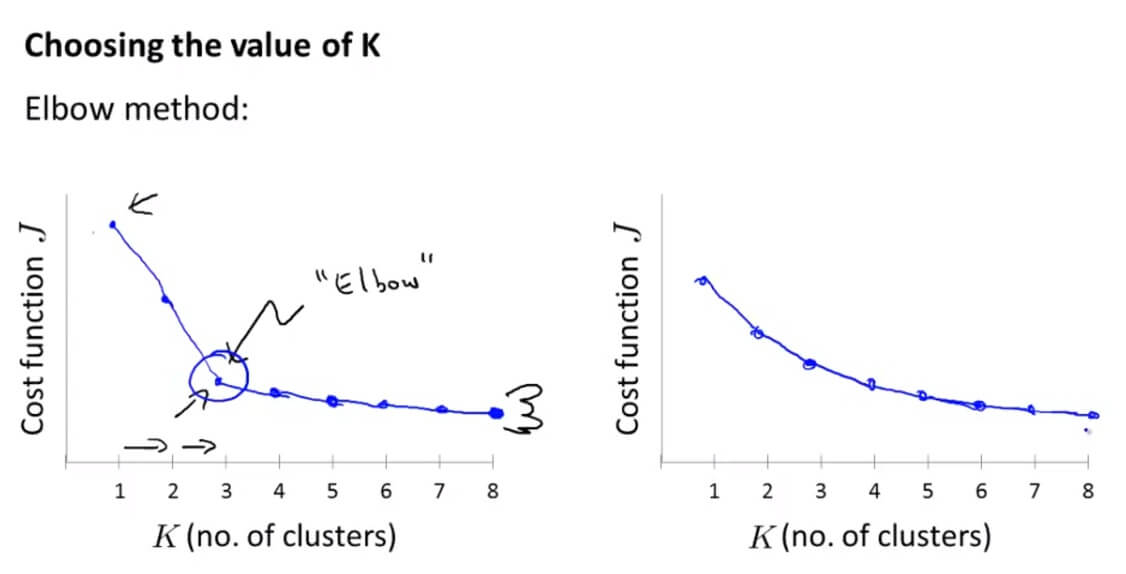
我们通过观察增加聚类中心的个数,其代价函数是如何变化的。有时候我们可以得到如左边的图像,可以看到在K=3的时候,有一个肘点(Elbow)。因为从1-3,代价函数迅速下降,但是随后下降比较缓慢,所以K=3,也就是分为3个类是一个好的选择。
然而,现实往往是残酷的,我们也会得到右边的代价函数,根本没有肘点,这就让我们难以选则了。
二. Unsupervised Learning 测试
1. Question 1
For which of the following tasks might K-means clustering be a suitable algorithm? Select all that apply.
A. Given a database of information about your users, automatically group them into different market segments.
B. Given sales data from a large number of products in a supermarket, figure out which products tend to form coherent groups (say are frequently purchased together) and thus should be put on the same shelf.
C. Given historical weather records, predict the amount of rainfall tomorrow (this would be a real-valued output)
D. Given sales data from a large number of products in a supermarket, estimate future sales for each of these products.
解答:A、B
A.前面的细分市场例子。
B.细分市场的实例。
C.给出历史的天气记录,那也就是说明确知道了真实值。属于监督学习。
D.同C。
2. Question 2
Suppose we have three cluster centroids $\mu_{1} = \begin{bmatrix} 1\ 2 \end{bmatrix}$, $\mu_{2} = \begin{bmatrix} -3\ 0 \end{bmatrix}$ and $\mu_{3} = \begin{bmatrix} 4\ 2 \end{bmatrix}$. Furthermore, we have a training example $x^{(i)} = \begin{bmatrix} 3\ 1 \end{bmatrix}$. After a cluster assignment step, what will $c^{(i)}$ be?
A. $c^{(i)} = 1$
B. $c^{(i)} = 3$
C. $c^{(i)} = 2$
D. $c^{(i)} $ is not assigned
解答:B
计算 $\frac{1}{m}\sum^{m}{i=1}\left | x^{(i)} - \mu{c}^{(i)} \right |^{2}$ 最小值,代入计算即可,B 选项是最小的。
3. Question 3
K-means is an iterative algorithm, and two of the following steps are repeatedly carried out in its inner-loop. Which two?
A. Using the elbow method to choose K.
B. The cluster assignment step, where the parameters $c^{(i)} $ are updated.
C. Feature scaling, to ensure each feature is on a comparable scale to the others.
D. Move the cluster centroids, where the centroids $\mu_{k}$ are updated.
解答:B、D
4. Question 4
Suppose you have an unlabeled dataset $\begin{Bmatrix} x^{(1)},\cdots,x^{(m)} \end{Bmatrix}$. You run K-means with 50 different random initializations, and obtain 50 different clusterings of the data. What is the recommended way for choosing which one of these 50 clusterings to use?
A. The only way to do so is if we also have labels y(i) for our data.
B. For each of the clusterings, compute $\frac{1}{m}\sum^{m}{i=1}\left | x^{(i)} - \mu{c}^{(i)} \right |^{2}$, and pick the one that minimizes this.
C. Always pick the final (50th) clustering found, since by that time it is more likely to have converged to a good solution.
D. The answer is ambiguous, and there is no good way of choosing.
解答: C
初始化选代价函数最小的。
5. Question 5
Which of the following statements are true? Select all that apply.
A. If we are worried about K-means getting stuck in bad local optima, one way to ameliorate (reduce) this problem is if we try using multiple random initializations.
B. Since K-Means is an unsupervised learning algorithm, it cannot overfit the data, and thus it is always better to have as large a number of clusters as is computationally feasible.
C. The standard way of initializing K-means is setting $\mu_{1},\cdots,\mu_{k}$ to be equal to a vector of zeros.
D. For some datasets, the “right” or “correct” value of K (the number of clusters) can be ambiguous, and hard even for a human expert looking carefully at the data to decide.
解答:A、D
A. 为了减少陷入局部最优的结果,可以多次选取随机初始参数。
B. 因为非监督学习没有过拟合所以可以选取更多的簇,那显然是不对的,不是越多的簇越好,而是看我们的要求的。
C. 初始化聚类中心应该是让其随机等于训练样本的值。
D. K值很难确定,正确。
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub
